“The Fourth Quadrant: No Realm for the Normal” summarizes Nassim Taleb’s description of the realm of the Black Swan, concluding that in this realm “normal” statistical metrics and associated risk management methods do not work and that redundancy, not optimization, is key to risk management. This Fourth Quadrant encompasses return distributions that have infrequent, large, unpredictable observations (shocks) that contribute materially to return distribution statistics. In the February 2011 version of his essay entitled “Antifragility, Robustness, and Fragility inside the ‘Black Swan Domain'”, he explores this realm further in the context of models as fragile (shocks involve largely negative returns) versus anti-fragile (shocks involve largely positive returns). For investors and traders, “model” means an investment strategy or a trading setup. Using a mostly theoretical approach, he argues that:
- Fragile models involve many small gains and infrequent massive losses, while anti-fragile models involve many small losses and infrequent massive gains (see the charts below). The former (latter) is like being short (long) an option.
- Models often contain assumptions that bias their forecasts in two ways:
- Misspecification or omission of higher order influences (non-linearities) tends to bias forecast errors in one direction over another.
- Forecast errors tend to amplify the importance of small-probability events (the infrequent, large, unpredictable observations, also termed distribution tail effects), especially when the distribution is “wild” and even when the distribution is “tame” (Gaussian).
- A common point of entry for such biases into models is treatment of a parameter (such as historical return distribution mean and standard deviation) as a constant rather than a stochastic variable (that may have non-zero higher order moments), as often done in applying Modern Portfolio Theory.
The following charts, taken from the essay, illustrate the payoff for fragile (upper chart) and anti-fragile (lower chart) Fourth Quadrant models over time. The former (latter) tends to bear shocks/model errors in a strongly negative (positive) way, equivalent to being short (long) an option and representative of the outcomes of an asymmetric distribution with a thicker left (right) tail. Model error/uncertainty fosters understatement of the importance of the large rare shock in the overall return for both series. Consequently, outcomes for the fragile (anti-fragile) model or strategy are actually less (more) attractive than investors generally estimate.
See “Strategy Test” for a detailed example of a fragile model. Its inverse would be an anti-fragile model.
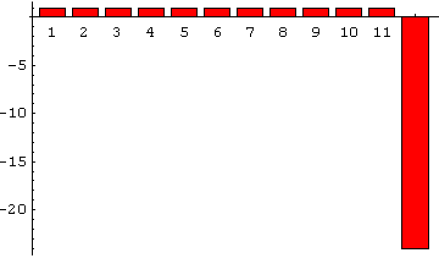
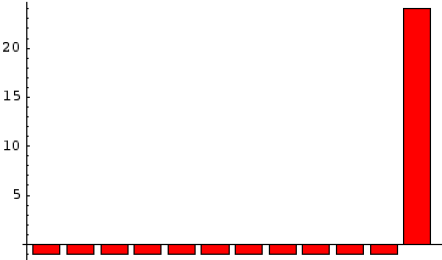
In summary, analysis suggests that widespread loose treatment of non-linearities in financial markets models (forecasting tools) tends to (1) bias forecasts in one direction and (2) amplify the importance of small-probability events, thereby enabling a contrarian approach of exploiting anti-fragility (strategies with infrequent, large, unpredictable positive payoffs).
In other words, anomalies (such as the variance risk premium) appear to exist because the investigators discovering them have not taken into account the biases implicit in their treatments of model error/uncertainty.
Cautions regarding conclusions include:
- Arguments are generally abstract, with no quantification of the potential profitability of exploiting anti-fragile, Fourth Quadrant strategies.
- Arguments do not address trading frictions, which are also variables with potentially non-linear influences that may work against such exploitation (trading frictions may rise dramatically around times of infrequent, large, unpredictable positive payoffs).