How much distortion can data snooping inject into expected investment strategy performance? In their October 2014 paper entitled “Statistical Overfitting and Backtest Performance”, David Bailey, Stephanie Ger, Marcos Lopez de Prado, Alexander Sim and Kesheng Wu note that powerful computers let researchers test an extremely large number of model variations on a given set of data, thereby inducing extreme overfitting. In finance, this snooping often takes the form of refining a trading strategy to optimize its performance within a set of historical market data. The authors introduce a way to explore snooping effects via an online simulator that finds the optimal (maximum Sharpe ratio) variant of a simple trading strategy by testing all possible integer values for strategy parameters as applied to a set of randomly generated daily “returns.” The simple trading strategy each month trades a single asset by (1) choosing a day of the month to enter either a long or a short position and (2) exiting after a specified number of days or a stop-loss condition. The randomly generated “returns” come from a source Gaussian (normal) distribution with zero mean. The simulator allows a user to specify a maximum holding period, a maximum percentage stop loss, sample length (number of days), sample volatility (number of standard deviations) and sample starting point (random number generator seed). After identifying optimal parameter values on “backtest” data, the simulator runs the optimal strategy variant on a second set of randomly generated returns to show the effect of backtest overfitting. Using this simulator, they conclude that:
- Computing power makes it is very hard to avoid backtest overfitting (trading strategies that falsely exhibit attractive performance), even when applied to purely random data.
- The in-sample/out-of-sample hold-out test method does not prevent backtest overfitting. With enough trials, a researcher can identify strategies that falsely perform well both in-sample and out-of-sample.
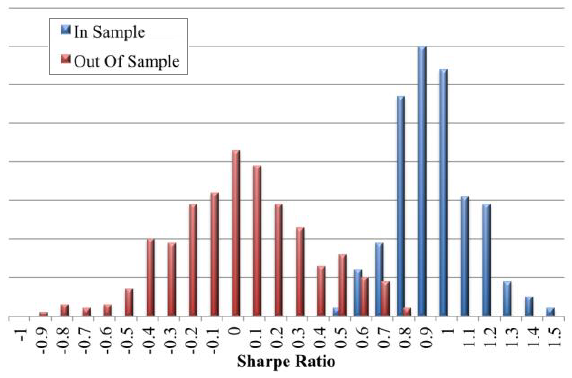
The following chart, taken from the paper, shows two distributions of annualized Sharpe ratios, each generated from 400 simulator trials.
In Sample: this distribution derives from simulator optimization of trading strategy parameter values to identify the strategy with the highest Sharpe ratio for each trial. Since the underlying data is randomly drawn from a normal distribution of “returns” with zero mean, the positive mean of the distribution derives entirely from snooping.
Out of Sample: this distribution of Sharpe ratios derives from 400 simulator trials of the optimized trading strategies with different random number generator seeds (new “return” series). This distribution has a mean Sharpe ratio of about zero, as expected in the absence of sample optimization.
Results indicate that snooping of data with no inherent patterns can easily mislead by generating attractive Sharpe ratios with no out-of-sample persistence.
In summary, results from simulations run on patternless data indicate that computing power makes it easy to be fooled by randomness.
Cautions regarding conclusions include:
- Normally distributed test returns differ from actual financial series that exhibit such features as autocorrelation, skewness and kurtosis (fat tails). Such non-normalities may support trading strategies that theoretically beat a market benchmark. However:
- Brute force refinement of such strategies may still introduce data snooping bias.
- Data non-normalities may not persist out-of-sample.
- On the one hand, the simulator represents worst case snooping bias by using data with no patterns. On the other hand the simulator does not represent worst case bias by considering a simple strategy (few parameters) and restricting parameter values to integers. The more complex the strategy, and the more values allowed for parameters during optimization, the greater the potential snooping bias.