Does mean-variance optimization reliably beat simple equal weighting? In his August 2012 paper entitled “The Efficiency of Mean-Variance Optimization with In-depth Covariance Matrix Estimation and Portfolio Rebalancing”, Joonas Hämäläinen tests how many of 96 different mean-variance optimization implementations based on daily data outperform simple equal weighting after accounting for trading frictions. He considers three methods of determining weights for minimum variance portfolios. For each method, he considers three historical intervals for estimating optimal portfolio weights (20, 60 and 250 trading days). He considers three fixed-interval (5, 20 and 60 trading days) and one threshold-based rebalancing rules. His benchmark strategy is equal weight, rebalanced weekly (EW). He tests strategy combinations on four sets of asset returns in euros constructed from 23 MSCI country indexes: 11 European Monetary Union markets during June 2002 through May 2006 (EMU1) and during June 2006 through May 2010 (EMU2); and, 12 big emerging markets during June 2002 through May 2006 (BEM1) and during June 2006 through May 2010 (BEM2). He assumes constant trading frictions of 0.2% (0.4%) of traded value for EMU (BEM) data sets. He focuses on annualized net Sharpe ratio (with risk-free rate zero) and portfolio turnover as critical evaluation metrics. Using daily country total return index levels during June 2001 through May 2010, with out-of-sample tests commencing June 2002, he finds that:
- Turnover for EW is very low, with little sensitivity to rebalancing frequency. Rebalancing every five trading days generates the highest average Sharpe ratio (0.62) across the four sets of returns.
- Minimum variance portfolios generally have higher turnover than EW.
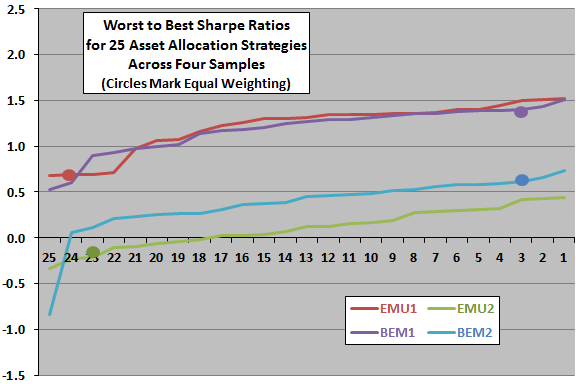
- Minimum variance portfolio performance relative to EW is mixed (see the chart below):
- 23 (22) of 24 minimum variance combinations beat EW for the EMU1 (EMU2) data sets.
- Two (two) of 24 mean-variance optimization combinations beat EW for the BEM1 (BEM2) data sets.
- Most minimum variance portfolios do have lower return standard deviations than EW.
- Based on raw predictive power, the optimal interval for estimating minimum variance portfolio weights is different for each dataset and rebalancing frequency, with short intervals yielding more accurate predictions than long intervals in most cases. However, short estimation intervals generate much higher turnover, such that medium and long estimation intervals produce the best portfolio outcomes. Overall, the 60-day historical interval beats the 20-day and 250-day intervals based on net Sharpe ratio.
- The best-performing portfolios entail relatively infrequent rebalancing to suppress trading frictions, with the threshold method most flexible.
- Picking the best estimation interval and the best rebalancing frequency appears to be more important than choosing the best estimation method.
The following chart, constructed from data in the paper, ranks the net Sharpe ratios generated by 24 minimum variance portfolios and the EW benchmark from lowest to highest for each of the four sets of stock index returns. Circles of matched colors indicate the position of the EW benchmark.
Results indicate that the EW benchmark is among the worst (best) for the EMU (BEM) samples, suggesting that the power of mean-variance optimization depends on sample properties. A possible interpretation is that mean-variance optimization works better when selected assets exhibit relatively high mutual return correlations, suggesting that the methodology may not be attractive for highly diversified assets.
In summary, evidence suggests that mean-variance optimization is sometimes superior to equal weighting and sometimes not, depending mostly on the set of assets considered.
Cautions regarding findings include:
- The study assigns no costs to the data collection and calculation burdens associated with minimum variance strategies.
- The study does not account for the data snooping bias associated with consideration of 24 combinations of minimum variance weighting estimation methods, estimation intervals and rebalancing frequencies for each set of data. Additional snooping bias may accrue to threshold rebalancing parameter selection. The aggregate bias may affect findings.
- Investors with relatively small portfolios may not be able to achieve assumed levels of trading friction, making EW relatively more attractive.
- While the study addresses trading frictions associated with rebalancing among indexes, it does not consider the costs (trading frictions and management fees) of creating tradable assets from indexes. These latter costs may vary materially across markets.
- Use of the Sharpe ratio as critical discriminator assumes well-behaved return distributions.
- The study considers only equities. Findings may not apply to sets of assets including other classes.
Frequently Asked Questions
What is mean-variance optimization and how does it differ from minimum variance portfolio construction?
Mean-variance optimization is a portfolio construction method that selects asset weights based on estimated returns, volatilities and correlations to balance expected return against risk. The article tests a minimum variance version, which focuses on minimizing portfolio return standard deviation using a covariance matrix estimated from historical daily data. It is typically compared against simple equal weighting.
Does mean-variance optimization beat equal weighting after trading costs?
Mean-variance optimization sometimes beats equal weighting after trading costs, depending mostly on the set of assets. In tests on 2002-2010 daily data, 23 of 24 and 22 of 24 minimum variance combinations beat equal weight for the two European Monetary Union samples, but only 2 of 24 did so for each of the two big emerging market samples. Net Sharpe ratios were calculated after assumed trading frictions of 0.2% (EMU) and 0.4% (emerging markets).
How are mean-variance optimization strategies tested against equal weight using historical data?
The study tested 96 implementations of mean-variance optimization (three weighting methods, three estimation intervals of 20, 60 and 250 trading days, and four rebalancing rules) against an equal-weight benchmark rebalanced weekly. Tests used daily total return data from 23 MSCI country indexes in euros, with out-of-sample testing starting June 2002 across four datasets. Performance was judged mainly by annualized net Sharpe ratio (risk-free rate zero) and portfolio turnover after trading frictions.
Does mean-variance optimization work better for highly correlated assets than for diversified ones?
Mean-variance optimization may work better when assets have relatively high mutual return correlations, according to a possible interpretation in the article. Equal weighting ranked among the worst strategies for European Monetary Union markets but among the best for big emerging markets, suggesting the optimization may be less attractive for highly diversified asset sets. This is an interpretation of the results, not a directly tested conclusion.
What are the limitations and risks of relying on minimum variance optimization instead of equal weighting?
The study's findings are limited by unaccounted data snooping bias from testing 24 combinations per dataset, plus possible extra bias from threshold rebalancing parameter selection. It also ignores data collection and calculation costs, the costs of creating tradable assets from indexes, and the higher trading frictions small investors may face, which favor equal weighting. The Sharpe ratio assumes well-behaved return distributions, and the study covers only equities, so results may not apply to other asset classes.