Can investors exploit greed among naive traders by selling them the most lottery-like equity options? In the March 2011 version of their paper entitled “Stock Options as Lotteries”, Brian Boyer and Keith Vorkink investigate the relationship between skewness of expected returns (a measure of prospects for extreme payouts, a proxy for “lotteryness”) and actual future returns for options on individual stocks. On the first trading day and the second Friday of each month, they create 40 option portfolios sorted first into eight expiration horizons and then into expected skewness quintiles. Based on end-of-day bid-ask midpoints, they calculate the return for each option assuming it is held to expiration (ignoring the possibility of early exercise) and returns for the 40 portfolios as the equally weighted average of constituent option returns. Using end-of-day bid and ask quotes, open interest and trading volume for options (screened for liquidity and obvious errors) and prices for the underlying U.S. common stocks during approximately 1996 through 2009, they find that:
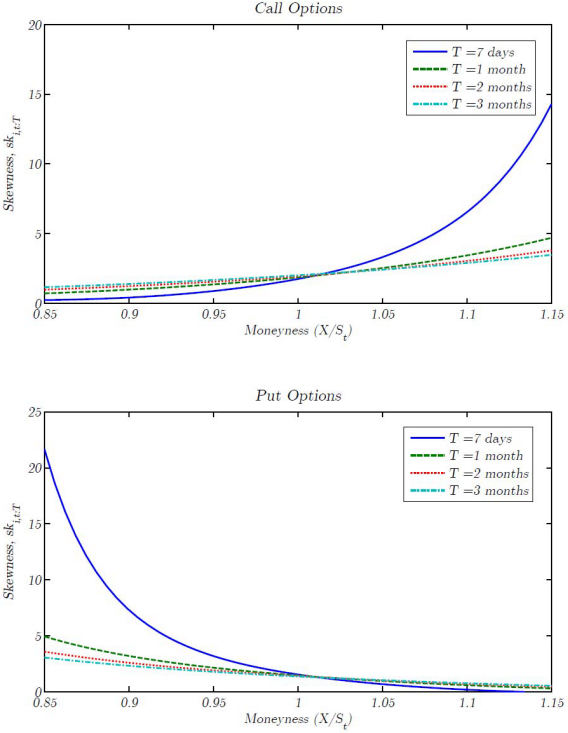
- Moneyness is the primary driver of expected return skewness, with expected returns of out-of-the-money options much more skewed than at-the-money or in-the-money options, especially as time-to-expiration decreases (see the charts below).
- Average returns for portfolios of options with low skewness are systematically greater than those for portfolios of options with high skewness, with low-high quintile spreads ranging up to about 60% per week. The average return spread between low and high skewness quintile portfolios:
- Is always positive for both calls and puts.
- Is always larger for puts than calls. For example, the spread is +1.4% minus -35.4%, or +36.8%, for calls expiring in seven days and -5.6% minus -60.6%, or +55.0%, for puts expiring in seven days.
- Increases as expiration horizon decreases (lottery-like characteristics emerge only near expiration).
- Trading in high-skewness options is largely demand driven. Option trading volume and open interest generally increase with expected return skewness, and a large fraction of trades in high-skewness options occurs above the bid-ask midpoint.
- Option bid-ask spread increases dramatically with skewness, implying that investors selling highly skewed options near the bid generally cannot capture the skewness premium. However, investors who write puts with high expected skewness appear to earn alphas of about 26% per week, perhaps because market makers can more easily hedge long put positions than long call positions.
- Findings are generally robust to controlling for market risks, trading activity and assumptions about return distributions.
The following charts, taken from the paper, plot expected return skewness for call (upper chart) and put (lower chart) options on individual stocks as functions of moneyness (horizontal axes) and expiration horizon (various values of T). Results illustrate the strong relationship between moneyness and skewness, especially as time-to-expiration decreases. In other words, skewness tends to be very high for far out-of-the-money options close to expiration for both calls and puts.
In summary, evidence indicates that investors may be able to exploit naive trader demand for highly skewed (lottery-like) payouts by selling well out-of-the-money put options on individual stocks.
Cautions regarding findings include:
- Maintaining return skewness expectations for a large number of individual stock options requires massive amounts of data and intensive computation. In other words, a rigorous search for opportunities would be costly. Many investors may want to use the moneyness and time-to-expiration shortcuts rather than calculate expected skewness.
- Returns reported ignore transaction fees for opening and closing (when in-the-money) positions. Including these frictions would lower reported returns.