Which stock market factors and stock characteristics contribute significantly to portfolio performance when considered jointly (accounting for interactions) on a net basis (accounting for offsetting trades)? In their February 2017 paper entitled “A Portfolio Perspective on the Multitude of Firm Characteristics”, Victor DeMiguel, Alberto Martin-Utrera, Francisco Nogales and Raman Uppal investigate which of 51 stock factors/characteristics matter on a net basis when considered jointly rather than individually. They focus on three research questions:
- Which characteristics are jointly significant from a portfolio perspective on an in-sample, gross basis?
- How does accounting for trading costs (an in-sample, net basis) affect the answer?
- Can investors exploit net findings out-of-sample?
They first construct single-characteristic hedge portfolios that are long (short) stocks with expected returns above (below) respective cross-sectional averages. They then construct a parametric multi-characteristic portfolio by adding to a benchmark portfolio the linear combination of single-characteristic hedge portfolios that maximizes mean-variance utility. They next determine which single-characteristic portfolio linear coefficients (the parameters) are significantly different from zero and decompose the contribution of each into gross return, risk and trading friction components. They measure the in-sample performance of a portfolio that exploits those characteristics with significant coefficients on a net basis. Finally, they perform an out-of-sample “big-data” strategy test that each month employs a rolling window of the last 100 months to specify the coefficients of the 51 long-short characteristic portfolios and holds the specified multi-characteristic portfolio the next month. They estimate proportional trading frictions for each stock as a function that decreases with each of two variables, market capitalization of the stock and time. Using monthly return and characteristics data for a broad sample of U.S. stocks (an average of about 3,000 per month) during January 1980 through December 2014, they find that:
- Tested separately, 21 (14) of 51 characteristics contribute significantly to a mean-variance utility goal on a gross (net) basis.
- Tested in-sample via an integrated, multi-characteristic portfolio on a gross basis, only six of 51 characteristics are significant.
- Five (unexpected quarterly earnings, volatility, asset growth, 1-month reversal and gross profitability) both increase average portfolio return and suppress portfolio volatility.
- One (least significant of the six, market beta) only suppresses portfolio volatility.
- Widely used 12-month momentum and book-to-market ratio are not significant because they do not boost portfolio average return enough to compensate for higher portfolio volatility.
- Tested in-sample via an integrated, multi-characteristic portfolio on a net basis, 15 of 51 characteristics are significant.
- Monthly portfolio reformation trades often offset, reducing the trading associated with individual characteristics by an average 65%.
- The most dramatic effect is for 1-month reversal, which has very high turnover. Combining this characteristic with the others as described reduces its trading frictions impact by 75%.
- Tested out-of-sample, the rolling window big-data strategy described above:
- Frequently picks the 15 significant in-sample characteristics (nine of the 10 characteristics most frequently selected are among these 15).
- Achieves net Sharpe ratio about 2.4 times that of value-weighted market, 2.0 times that of a parametric portfolio exploiting size, book-to-market and 12-month momentum characteristics and 1.25 times that of a parametric portfolio exploiting size, book-to-market, asset growth and gross profitability (see the chart below).
- Generates monthly net alphas around 1% relative to widely used 4-factor (either market, size, book-to-market and momentum; or, size, book-to-market, asset growth and gross profitability) and 5-factor (market, size, book-to-market, investment and gross profitability) models of stock returns.
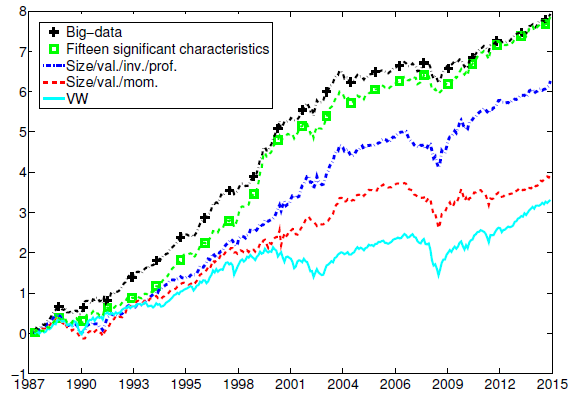
The following chart, taken from the paper, compares net cumulative returns during the out-of-sample test period of five portfolios:
- Big-data – the out-of-sample big-data parametric portfolio strategy employing all 51 characteristics as specified above.
- Fifteen significant characteristics – a parametric portfolio combining the 15 characteristics found to be significant in-sample (with attendant look-ahead bias).
- Size/val./inv./prof. – a parametric portfolio combining size, book-to-market, investment and gross profitability characteristics.
- Size/val./mom. – a parametric portfolio combining size, book-to-market and 12-month momentum characteristics.
- VW – the value-weighted market portfolio.
For comparability, the authors apply leverage as needed so that returns for all portfolios have the same volatility. The striking result is that the out-of-sample big-data strategy generates a Sharpe ratio similar to that of the portfolio based on the 15 in-sample significant characteristics.
In summary, evidence indicates that portfolios integrating characteristic-based stock selections makes more characteristics useful because of offsetting trades.
Cautions regarding findings include:
- The authors consider trading frictions, but not:
- Shorting costs/constraints in the characteristic hedge portfolios. Shorting for some stocks may be costly or precluded due to lack of shares available to borrow.
- Cost of leverage as applied in the chart above to standardize portfolio volatility.
- The out-of-sample portfolio management process is daunting, and investors would bear fees for delegating the process to a fund manager.
- Timely data collection, data processing and portfolio reformation trade executions seem problematic, especially with resources available early in the sample period.
- The portfolio construction approach is elaborate, impounding risk of secondary snooping bias (inherited from prior studies) and creating many opportunities for snooping model construction and assumptions. Even out-of-sample testing can include snooping bias if informed by iterative test runs. The level of complexity argues for live testing.
See also the following related research summaries: