A reader inquired: “In some technical analysis papers I read that trend reversals of the 10-day [lagging] average put-call ratio anticipate S&P 500 index trend reversals. Do you see any predictive power?” In other words, does a change in the trend on an index put-call ratio (P/C) predict a general shift in investor sentiment? This question is fairly complicated from an analysis perspective, requiring definitions of “trend,” “trend reversal” and “anticipate.” We define “trend” as the normalized slope for the last ten trading days for both the S&P 500 index and the ten-day lagging average index P/C over the past ten trading days, normalizing by dividing the raw slope by the average value over the same ten trading days. We define “trend reversal” as a point at which the normalized slope crosses zero either from above or below (slope changes from positive to negative or negative to positive). We define “anticipate” as evidence of a systematic relationship between points at which the normalized slope of the ten-day average P/C changes sign and points at which the normalized slope of the S&P 500 index changes sign in the same direction. Using daily P/C data for the S&P 500 index from CBOE for the period 10/17/03 through 1/9/08 (1,317 trading days) and contemporaneous daily closing levels of the S&P 500 index, we find that:
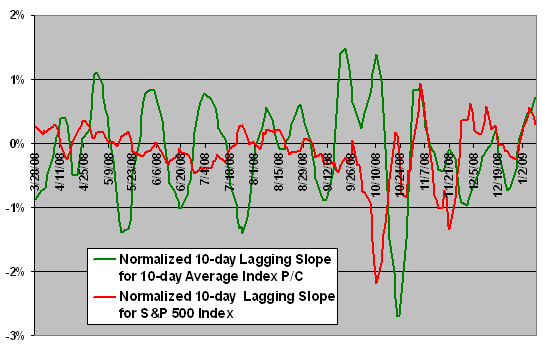
The following chart shows the behaviors of both trends over the last 200 trading days in the sample. Visual inspection does not reveal any systematic relationship between the points at which the slopes of the two trend lines change sign in the same direction. No systematic relationship of any kind is obvious.
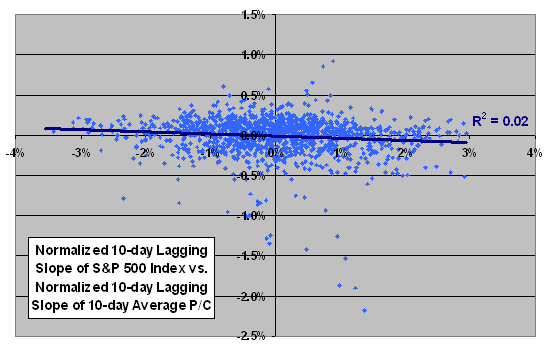
Presumably, if the crossover points relate systematically, the entire series of the two trends should relate systematically. The following scatter plot relates the normalized 10-day lagging slope of the S&P 500 index to the normalized 10-day lagging slope of the 10-day lagging average P/C for the S&P 500 index over the entire sample period. The Pearson correlation for the two series is -0.13. The R-squared statistic is 0.02, indicating that variation in the P/C trend explains just 2% of the variation in the index trend. These statistics barely change if we assume that the P/C trend leads the S&P 500 index trend by five or ten trading days.
There is considerable sampling interval overlap in the raw data. After winnowing the sample to reduce overlap by taking every tenth data point (130 surviving sample points), the R-squared statistic is 0.01. If we offset the two series such that the P/C trend leads the S&P 500 index trend by ten trading days for this winnowed sample, the Pearson correlation and R-squared statistic are approximately zero, indicating no relationship.
We could try different definitions of “trend,” “trend reversal” and “anticipate”, at the risk of incorporating data mining bias into results.
In summary, evidence from a few tests does not support a belief that trend reversals in the 10-day lagging average S&P 500 index put-call ratio predicts reversals in the level of the S&P 500 index.