Are value and momentum anomalies reliably present across international asset classes? If so, can investors exploit them to generate abnormal returns? In the December 2007 version of their paper entitled “Global Tactical Cross-Asset Allocation: Applying Value and Momentum Across Asset Classes”, David Blitz and Pim van Vliet examine global tactical asset allocation strategies across a broad range of asset classes based on both value (asset yield or earnings yield) and momentum (both short-term and long-term). These strategies weight asset classes according to volatility, with higher (lower) weights assigned to classes with lower (higher) volatilities. Using price and yield data for 12 international asset classes spanning January 1985 through September 2007, they conclude that:
- Hedge, or zero-investment, portfolios that are long (short) the top (bottom) quarter of asset classes, rebalanced monthly over the entire sample period, generate average annual returns before transaction costs of:
- 4.4% based on valuation;
- 5.0% based on 12-1 momentum (calculated from the past 12 months excluding the most recent month); and,
- 7.4% based on 1-month momentum.
- Correlations among the returns of these strategies are fairly weak (and negative between valuation and the two types of momentum), suggesting distinct effects.
- A hedge portfolio that is long (short) the top (bottom) quarter of asset classes based on a combination of valuation and momentum generates an annualized return of over 9% before transaction costs (perhaps 7% after transaction costs) over the entire sample period.
- Outperformance of this strategy is stable over time and present in a 1974-1985 out-of-sample test on a reduced set of asset classes.
- The return cannot be explained as a reward-for-risk proposition using commonly used risk factors (market, size, value and momentum).
- Financial markets at the asset class level may be inefficient because there is not enough “smart money” to eliminate mispricings.
The following chart, taken from the paper, presents the cumulative performance of the individual and combination hedge portfolios described above. It shows that the performance of the portfolios is generally stable across the entire sample period.
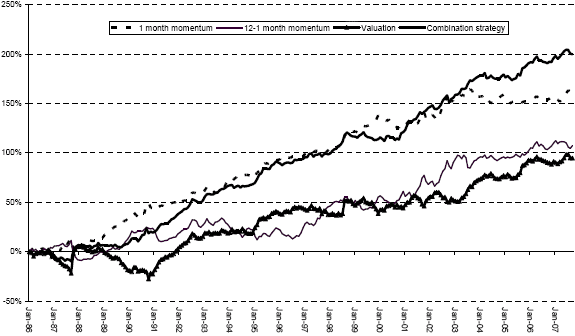
In summary, value and momentum investing may work across a broad range of asset classes, and the two effects are independent enough that combining them may yield incremental outperformance.
A reader asked: “I’m really interested in applying this strategy, but after reading through it several times I still don’t understand how to apply it. Can you restate the strategy in simpler terms?”
The strategy, summarized in “Combined Value-Momentum Tactical Asset Class Allocation”, defines attractive and unattractive asset classes by ranking 12 classes based on a combination of momentum and value measurements. Specifically, quoting from the paper:
“At the end of every month we rank all assets based on their momentum and/or valuation scores, and use this ranking to assign the assets to four quartile portfolios consisting of three assets each. We then calculate the return of each quartile portfolio over the following month.” The use of quartiles is somewhat arbitrary, trading purity of attractiveness/unattractiveness for diversification.
To rank assets for the momentum-only strategies tested in the paper:
“We will examine both a 1-month return strategy and a classic 12-1 month (12 months excluding the most recent month) momentum strategy.”
To rank assets for the valuation-only strategy tested in the paper:
“The starting point of our approach is to take a simple yield measure for each asset class. …we apply a limited number of asset-specific, fixed adjustments to the basic yield data. These adjustments were chosen in such a way that the main structural biases towards certain asset classes are removed. …these adjustments result in scores that are much more comparable across asset classes. In fact, after applying the adjustments, the long-term average valuation score for every asset falls in a range between -1% and +1%, which implies that structural biases towards certain asset classes are effectively eliminated.”
To rank assets for the combined momentum-valuation strategy tested in the paper (the one that interests you):
“A combined score for each asset class is calculated by taking a weighted average of its rank (1 to 12) on the individual variables. We choose a simple 50/50 balance between the momentum and valuation strategies and equal weighting of the two momentum variables. This translates into weights of 25% for 1-month momentum, 25% for 12-1 month momentum and 50% for valuation.”
For example, if a certain asset class ranks 4th for 1-month momentum, 8th for 12-1 momentum and 6th for valuation, its combined rank would be: 0.25*4 + 0.25*8 + 0.5*6 = 6. A portfolio that is long the assets with the top three combined ranks and short the assets with the bottom three combined ranks, reformed monthly, generates the 11.9% annual return (before trading frictions) stated in the paper. The use of 25%/25%/50% weights is arbitrary.
The yield adjustments that allow ranking different asset classes by valuation vary by asset class. Specifically:
- “for the government bond assets, US Treasuries and German and Japanese government bonds, we subtract 1% from the term premiums, which adjusts for the fact that the yield curve tends to be upward sloping;
- “for US investment grade credits we subtract 2% and for US high yield bonds 6%, also to adjust for the slope of the yield curve, and additionally to adjust for default risk;
- “for emerging markets equities we subtract 1% to adjust for the structurally lower P/E compared to mature equity markets;
- “for US real estate equities we subtract 2% to adjust for the structurally higher yield compared to regular equities.”
You would have to construct and maintain an adjusted yield dataset for each asset class of interest. If you introduce asset classes beyond those used by the authors, you would have to determine appropriate yield adjustments for them. You could probably do the yield adjustments empirically (instead of top-down, as the authors do) by picking a base asset class (e.g., U.S. equities) and regressing yields from other classes against the yield of the base class to derive adjustments. The yield adjustments are perhaps the hardest part of the approach.