A reader inquires: “Ken Fisher did a statistical study in his book, The Only Three Questions That Count: Investing by Knowing What Others Don’t, which states that growth (value) is in favor when the yield curve flattens (steepens). Any truth to this?” To test this hypothesis, we compare the performances of paired growth and value indexes/funds as the spread between the yields on the 10-year Treasury Note (T-note) and the 90-day Treasury Bill (T-bill) varies. Using monthly and quarterly adjusted (for dividends) return data for a pair of growth-value indexes and a pair of growth-value mutual funds, along with contemporaneous T-note and T-bill yield data, we find that:
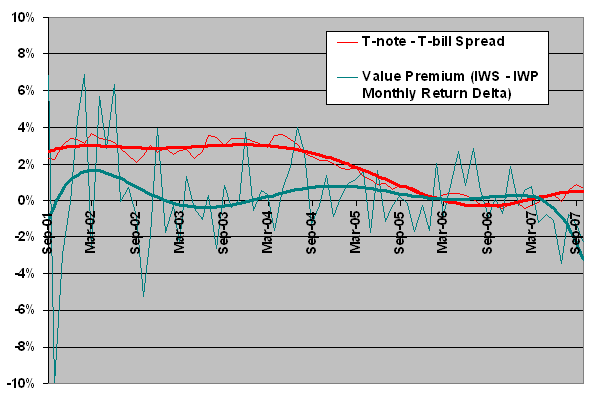
The following chart compares the monthly T-note/T-bill yield spread to a “value premium” defined as the monthly adjusted return of the iShares Russell Midcap Value Index (IWS) minus the monthly adjusted return of the iShares Russell Midcap Growth Index (IWP) over the period 9/01 through 10/07 (74 months of data). The jagged lines are the raw data, showing that the value premium is very noisy on a monthly basis. The heavy lines are sixth-order polynomial best fits for the two series. It is not obvious that there is a relationship between the yield spread and the value premium for this sample based on this visualization.
For a closer look, we compare the monthly returns for the two indexes to the monthly change in the yield spread.
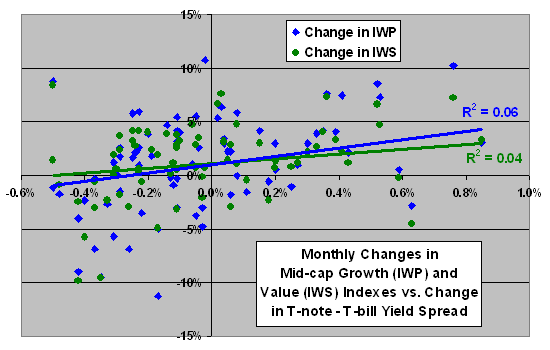
The following scatter plot relates monthly changes in IWP and IWS to the monthly change in the T-note/T-bill yield spread over the same period. Results indicate that both indexes tend to perform better (worse) as the yield spread grows (shrinks). The Pearson correlations for the IWP and IWS series are 0.25 and 0.19, respectively. The R-squared statistics for these series are 0.06 and 0.04, suggesting that yield spread changes have very little power to explain either growth or value stock monthly returns.
The relative positions of the best-fit lines using monthly data over six years do not support Ken Fisher’s hypothesis, with growth (value) stock returns tending to be higher when the yield spread is growing (shrinking). However, the difference in the best-fit lines is small.
Excluding September/October 2001 as outliers increases correlations and R-squareds, and increases the difference in slope between growth and value best-fit lines without affecting relative positions.
Might the differences between growth and value stock reactions to yield spread changes be more apparent on a quarterly basis?
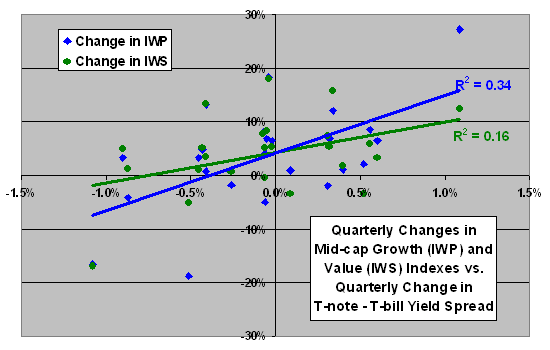
The next scatter plot relates quarterly changes in IWP and IWS to the quarterly change in the T-note/T-bill yield spread starting in September 2001 (24 quarters). Results indicate that both indexes tend to perform better (worse) as the yield spread grows (shrinks). The Pearson correlations for the IWP and IWS series are 0.58 and 0.41, respectively. The R-squared statistics for these series are 0.34 and 0.16, suggesting explanatory power for yield spread changes over quarterly intervals.
The slope of the best-fit line for IWP (growth) remains steeper than that for IWS (value), and the relative positions of the best-fit lines again do not support the hypothesis. Growth stocks appear to like a widening yield spread more than do value stocks, and value stocks appear to outperform when the yield spread shrinks.
The time period considered so far probably constitutes less than one full contraction-expansion economic cycle and may be unrepresentatively influenced by the unusually severe 2000-2002 bear market. Might a longer time series say something different about the reactions of growth and value stocks to changes in the yield spread?
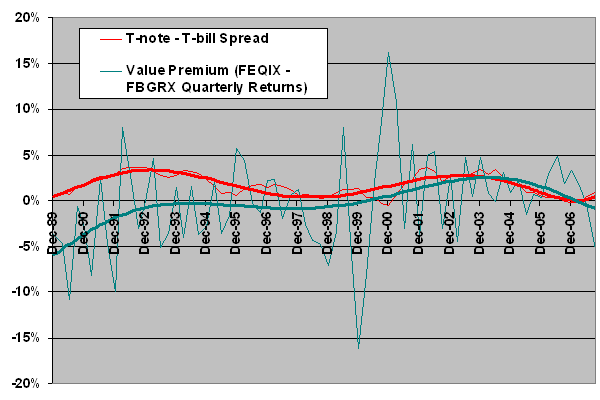
The next chart compares the quarterly T-note/T-bill yield spread to a “value premium” defined as the quarterly adjusted return of the Fidelity Equity-Income (FEQIX) mutual fund minus the quarterly adjusted return of the Fidelity Blue Chip Growth (FBGRX) mutual fund starting in September 1989 (72 quarters). The jagged lines are the raw data, showing that the value premium is still very noisy on a quarterly basis. The heavy lines are sixth-order polynomial best fits. Visual inspection suggests that there may be a relationship between the yield spread and the value premium over this longer sample period. The shapes of the best-fit curves are broadly similar.
For a closer look, we compare the quarterly returns for the two funds to the quarterly change in the yield spread.
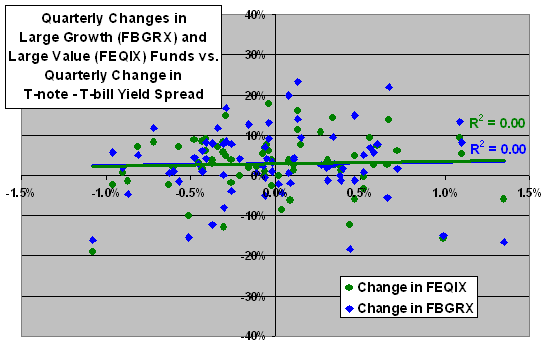
The final scatter plot relates the quarterly changes in FBGRX and FEQIX to the quarterly change in the T-note/T-bill yield spread since September 1989. Results indicate no relationship between mutual fund returns and the yield spread. The Pearson correlations for the FBGRX and FEQIX series are 0.01 and -0.03, respectively. The R-squared statistics for both series are 0.00.
The lack of differences between growth and value for this longer sample period provide no support for the hypothesis.
Offsetting the data series such that quarterly changes in the yield spread lead quarterly fund returns by one to eight quarters produces no clear, consistent relationships.
In summary, limited analyses do not support the hypothesis that growth (value) stocks systematically outperform when the T-note/T-bill yield spread shrinks (grows).
Note that the variables chosen to represent the yield spread, growth stock returns and value stock returns may not be optimum for testing the hypothesis. Portfolios more extremely tilted toward growth and value might provide a stronger test. Also, the samples may not be long enough to capture a difference in economic-cycle effects on growth and value stocks.
Two readers sent the following elaboration of Ken Fisher’s hypothesis:
Ken Fisher in his book says that there is no relationship between the U.S. yield curve and relative strength for growth versus value stocks. He claims that there is a growth-versus-value indication from the world yield curve, calculated as a GDP-weighted average of the yield curves of the major economies.
Here are three points in response:
- Skepticism about long-run inference from yield curves is warranted because it is very difficult to assemble reasonably large, reliable, independent samples in terms of number of economic cycles. Capturing 20 economic cycles (yield curve cycles) requires using data so old that its relevance is questionable in terms of financial, regulatory and technological environment. It is arguable that economic cycles do not exist under any robust and rigorous definition – too many moving parts and interdependencies.
- Testing many variations of yield curves (national-international, weighted-unweighted, duration selection) introduces data mining bias, meaning that the optimum curve criteria (best R-squared) likely generate “lucky” results with overstated predictive power.
- If forecasting based on yield curve analysis has a sound logical basis, should not the yield curve for a major economic entity have at least some effectiveness?