Standard deviation is likely the most widely used measure of investment risk, but quadratic dispersion from the mean not be the most intuitive measure. There is evidence that investors confuse standard deviation with mean absolute deviation, and they may further misinterpret standard deviation due to its “normal” association with the Gaussian distribution (inapplicable for some financial data series). Would some other baggage-free measure of risk make more sense to investors? In his November 2008 paper entitled “The Gain-Loss Spread: A New and Intuitive Measure of Risk”, Javier Estrada proposes the gain-loss spread (GLS) as an intuitive and useful measure of investment risk. GLS is the difference between the expected gain (probability of gain times average gain) and the expected loss (probability of loss times average loss). Using monthly return data for 49 country indexes (22 developed and 27 emerging) and 57 industry indexes from initial availability through December 2007, he concludes that:
- GLS correlates strongly with standard deviation, providing essentially the same information about volatility.
- GLS correlates more strongly with mean returns for country and industry indexes than do standard deviation and beta with respect to a world index, providing a tighter link between risk and return.
- GLS discriminates between high-risk and low-risk portfolios better than beta and at least as well as standard deviation (see the table below).
- An investment strategy based on GLS is profitable and comparable to (better than) a strategy based on standard deviation (beta).
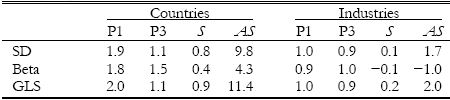
The following table, taken from the paper, shows mean returns, spreads in mean returns (S) and annualized spreads in mean returns (AS) in percent for country and industry indexes grouped into three equally-weighted portfolios based on three measures of risk: standard deviation (SD), beta with respect to the MSCI World index (Beta) and GLS. In each case, group P1 (P3) is the riskiest (least risky). Results show that GLS is much better than Beta and at least as good as SD in extracting the risk-return relationship for equities. For example, the riskiest third of country indexes outperform the least risky third of country indexes by an annualized 11.4% using GLS to define risk, but only 9.8% and 4.3% using SD and Beta, respectively, to define risk.
In summary, gain-loss spread (expected gain minus expected loss) is a simple, intuitive measure of investment risk at least as useful as standard deviation.