Practical Capture of the Volatility Risk Premium?
July 10, 2025 - Volatility Effects
Can investors safely capture the U.S. stock market volatility risk premium (VRP), the tendency of implied volatility to exceed realized volatility. In their June 2025 paper entitled “The Volatility Edge, A Dual Approach For VIX ETNs Trading”, Carlo Zarattini, Andrew Aziz and Antonio Mele concisely review the history of volatility trading. They then investigate whether investors can capture some of VRP via the following four progressively constructed strategies (table from the paper):
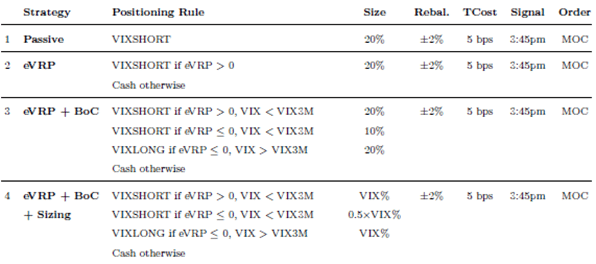
- Strategy 1 is a benchmark, a continuous 20% position in VIXSHORT (modeled from the S&P 500 VIX Short-Term Futures Inverse Daily Index with 0.80% annual fee). The remaining 80% is in cash with no earned interest. Rebalancing occurs via market-on-close (MOC) trades whenever the VIXSHORT allocation drifts from 20% by at least 2% as measured daily at 3:45pm, with 0.05% trading frictions (Tcost).
- Strategy 2 is the same as Strategy 1, except the VIXSHORT allocation is made only when the expected VRP (eVRP) is positive when measured daily at 3:45pm as VIX minus the annualized standard deviation of 10-day (3:45pm) SPDR S&P 500 ETF (SPY) returns.
- Strategy 3 adds a signal to Strategy 2, with allocations to VIXSHORT or VIXLONG (modeled from S&P 500 VIX Short-Term Futures Index Total Return with 0.50% annual fee), depending on whether the 3:45pm VIX term structure is in backwardation or contango (BoC), meaning that 90-day implied volatility (VIX3M) is less than or greater than VIX.
- Strategy 4 replaces the fixed allocations in Strategy 3 with allocations based on the 3:45pm level of VIX.
Using daily and 1-minute intraday data for the specified input variables during January 2005 through May 2025, they find that: