How does volatility interact with market beta? In his 2012 paper entitled “Volatility and Compounding Effects on Beta and Returns”, William Trainor investigates the performance of stocks sorted on market beta overall and during intervals of low and high market volatility. He considers both ideal (theoretical) betas and betas estimated from lagged returns. He defines low (high) market volatility as below (above) the long-term annual average for a value-weighted index constructed from a broad sample of U.S. stocks (15.8%). Using both theoretical derivations and empirical monthly returns for sampled stocks during January 1926 through December 2009, he finds that:
- Theoretically, higher-beta stocks outperform lower-beta stocks when market volatility is low, but roles reverse when market volatility is high. In fact, when market volatility is high, compounding effects should make high-beta stocks underperform the market (see the first chart below).
- Empirically, annually reformed and equally weighted high-beta portfolios outperform (underperform) low-beta portfolios by 0.42% (0.51%) a month when market volatility is low (high). After combining volatility environments over the long run, there is no significant relationship between beta and return (see the second chart below).
- Moreover, a simple trading rule that holds high-beta (low-beta) stocks when prior-month market volatility is below (above) its five-year average performs about the same as buying and holding either the high-beta or the low-beta portfolio. More sophisticated models of future volatility may work better.
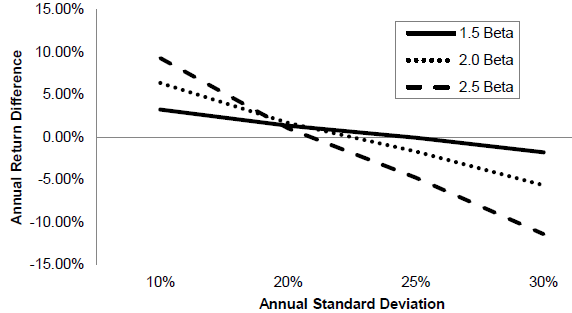
The following chart, taken from the paper, summarizes the theoretical interaction of market volatility, a portfolio’s market beta (1.5, 2.0 or 2.5) and the portfolio’s annual market-adjusted return. Theoretical assumptions are: (1) the market follows a random walk (has a tame return distribution) around a long-term 8% annualized (geometric mean) return; and, (2) portfolio beta is constant during the measurement year. The ideal relationship between a portfolio’s beta and its excess return is positive (negative) when annual market volatility is below (above) about 20%. A portfolio with beta 1.5 (2.5) underperforms the market when market volatility exceeds about 25% (21%).
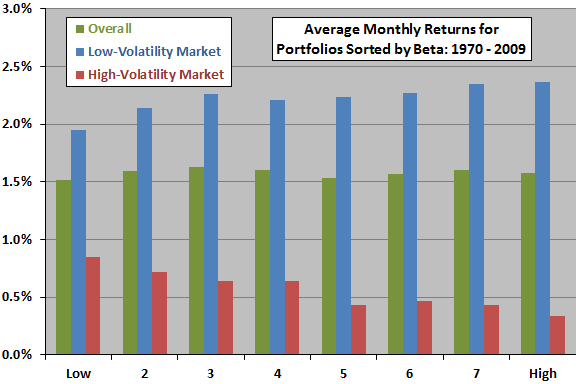
The next chart, constructed from data in the paper, summarizes average monthly returns for eight equally weighted portfolios sorted annually on prior year beta (excluding extreme lowest-beta and highest-beta portfolios) during 1970 through 2009 overall, and during low-volatility and high-volatility market environments. Portfolio betas range from a low of 0.67 to a high of 1.42. Low-beta (high-beta) stocks tend to outperform when market volatility is high (low), such that there is no discernible overall relationship between beta and return.
In summary, theoretical derivation and empirical evidence indicate that a portfolio’s beta may not be useful in predicting its long-run return due to interaction of beta and time-varying volatility, but beta may be a useful metric for investors who can predict market volatility.
Cautions regarding findings include:
- Returns are gross, not net. Including reasonable trading frictions for construction and periodic reformation would reduce reported returns for all portfolios.
- The 15.8% threshold for low/high volatility is an in-sample determination. An investor operating in real time based strictly on historical data would set different thresholds over time.
- Dropping the extreme highest-beta and lowest-beta portfolios for the second chart above may distort overall relationships and be at odds with the experiences of some investors.