Both the academic community and practitioners generate large numbers of studies, formal and informal, analyzing and forecasting financial markets. In this blog, we offer an organization of financial markets research by topics such as The Value Premium and Buybacks and Secondaries. Are there other organizing principles that might convey a more fundamental understanding? Reflecting on the hundreds of studies we have reviewed and the limitations of this research with regard to practical application, here is another framework for thinking about financial markets research:
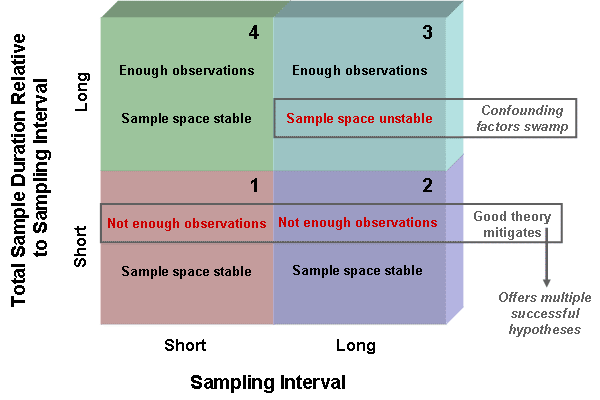
The following figure summarizes a way of thinking about financial markets research that emphasizes the sampling interval (short-term or long-term data collection and prediction) and the sample duration (number of sample intervals), as follows:
Quadrants 1 and 2 address sample durations that are short in comparison with sampling intervals (e.g., five years of annual stock market returns, or two weeks of daily stock returns). In general, studies in these categories sacrifice the reliability of a large number of independent observations for the ease and comfort of readily collected and compared data. Building a Quadrant 1 or 2 study on a good theory mitigates the statistical shortcoming of a small number of observations. A good theory does not mean a story that is just plausible or entertaining, but rather a story that generates multiple successful hypotheses. Even though each hypothesis may suffer from limited test data, aggregate successful testing across all hypotheses indicates reliability.
Quadrants 3 and 4 address sample durations that are long in comparison with sampling intervals (e.g., 100 years of annual stock returns, or ten years of weekly market sentiment measures). These studies incorporate the inherent statistical reliability of large samples, but very long durations risk confounding factors that disrupt the hypothesis.
Quadrants 1 and 4 address short-interval testing, achieving the granularity necessary for short-term predictions. These studies allow large samples without very long overall sample durations.
Quadrants 2 and 3 address long-interval testing, sacrificing granularity in order to investigate big issues (e.g., calculating the equity risk premium or testing value versus growth or finding bull-bear market turning points based on a business cycle). However, these studies face the trade-off between small samples and instability of the testing environment. A recent investing/trading environment may be fundamentally different from a distant past one with quite different kinds of investment vehicles, regulations and information-moving technologies. In addition, old data may be of dubious quality.
How about some examples?
Examples:
Quadrant 1: Short-term overbought/oversold indicators fit in this quadrant. Outputs have low inherent statistical reliability.
Quadrant 2: A specific example for this quadrant is the examination of calendar effects by stock market sector. Data for funds tracking performance by sector are readily available for just a few years, not enough for reliable statistical inference over future one-year periods.
Quadrant 3: Annual return estimates based on 101 years of annual data are statistically sound. However, the quality of data fades into the past, and the influences of secular trends in financial sophistication, regulation and information technology are arguable.
Quadrant 4: An example for this quadrant is the analysis of the positions of traders in S&P 500 index futures. This analysis covers 12 years of weekly data and draws conclusions about short-term stock market behavior.
Studies with extremely long sampling intervals (based on the business cycle or demographics) suffer the shortcomings of both Quadrants 2 and 3. Comparable data is generally unavailable across many sampling intervals, and confounding factors may vary dramatically across just a few sample intervals. Theory with multiple testable hypotheses is important to such studies.
In general, forecast intervals should be comparable to sampling intervals. Some studies (or, more accurately, casual punditry) use short-term data to predict long-term market behavior, often by referring to a few extreme data points. This approach gives the illusion of large sample size, but the sample data points are not independent (the same data points feed many overlapping forecast intervals). If such studies instead properly matched sampling intervals to long-term forecast intervals, it would be obvious that they fall into observation-starved Quadrant 2.
In summary, the uses of empirical research on financial markets derive in large measure from sampling frequency (supporting either short-term or long-term prediction) and sample duration (supporting either reliable or unreliable inference).