Are there systematic errors in market expectations about the future volatilities of individual stock prices? If so, what reliable strategy could a trader use to exploit these errors? In their August 2006 paper entitled “Option Returns and the Cross-Sectional Predictability of Implied Volatility”, Amit Goyal and Alessio Saretto examine the complete range of implied stock price volatilities for all U.S. equity options to devise an volatility forecasting model more efficient than that inherent in the market. They then test the model’s ability (out of sample) to identify outperforming options trading strategies that exploit this market inefficiency. Using daily data for all U.S. equity options over the period January 1996 to May 2005, they conclude that:
- A stock with an implied volatility below (above) the average for all stocks and below (above) its own twelve-month moving average implied volatility has a higher (lower) implied volatility in the next month. This prediction is more accurate than that deduced from actual options prices (the market is not completely efficient, perhaps overreacting to the latest information).
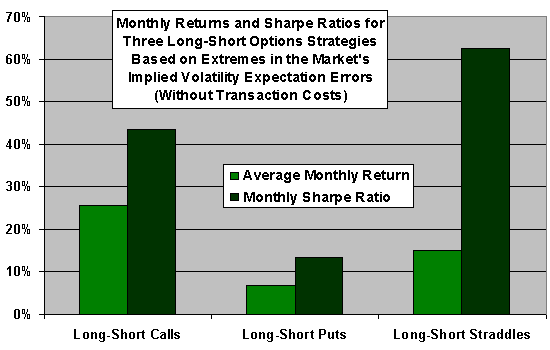
- A trading strategy that is long (short) at-the-money, one-month-to-maturity straddles for stocks with the largest expected positive (negative) changes in implied volatility yields a statistically and economically significant average monthly return of 15.0% and monthly Sharpe ratio of 0.626. Assuming transaction costs of half the quoted options bid-ask spreads, this average return of 15.0% falls to 5.3% per month. However, focusing on stocks with less liquid options boosts this 5.3% to 6.7% per month.
- The long-short straddles portfolio performs better when aggregate market volatility (VIX) is increasing than when it is decreasing.
- These results hold for different market conditions, firm risk characteristics, industry groupings and options liquidity characteristics. However, average returns are higher for high beta, small market capitalization and past loser stocks.
The following chart, constructed from data in the paper, depicts average monthly returns and Sharpe ratios for the straddle strategy described above and for similar strategies using either calls only or puts only. All three strategies are long (short) at-the-money, one-month-to-maturity options for stocks with the largest expected positive (negative) changes in implied volatility. Returns assume an average of the bid and ask quotes as a beginning price and the expiration payoff of the option (based on the stock price at expiration and the strike price) as the ending price. The chart shows that call options produce the largest raw returns, but straddles offer fairly large raw returns with a much smaller standard deviation and hence a larger Sharpe Ratio.
In summary, a market inefficiency with respect to volatility expectations for individual stocks may provide a means to beat the market by using options to trade volatility.
See the CBOE Trading Tools for basic implied and historical (actual) volatility data.
Note that the above trading strategy requires access to and frequent processing of large datasets, and that it is a statistical approach that assumes many concurrent positions. Individual investors/traders may be able to apply the basic principles to define some simpler options trading guidelines — for example, focusing on stocks for which implied volatilities are currently extraordinarily high or low compared to the past and likely to exhibit mean reversion.