Does the options-based expected volatility of the expected volatility of the S&P 500 Index (expected volatility of VIX, or VVIX) convey useful information about future returns of related assets? In their April 2017 paper entitled “The Volatility-of-Volatility Term Structure”, Nicole Branger, Hendrik Hülsbusch and Alexander Kraftschik investigate the VVIX term structure via principal component analysis. They interpret the first, second and third principal components of the term structure as its level, slope and curvature, respectively. They examine relationships between the VVIX term structure and returns on S&P 500 Index option straddles and VIX option straddles. Using groomed daily prices for S&P 500 Index options and VIX options with maturities 1, 2, 3, 4 and 5 months, and daily excess returns of at-the-money delta-neutral S&P 500 Index straddles with maturities 1, 2, 3, 6, 9 and 12 months and VIX straddles with maturities 1, 2, 3, 4 and 5 months during September 2007 through August 2014, they find that:
- As for VIX, VVIX relates negatively to S&P 500 Index returns, and financial and economic shocks relate to jumps in VVIX.
- The VVIX term structure slopes downward 95% of the time (see the chart below), indicating that investors usually expect it to decrease.
- The level and slope components of the VVIX term structure explain 98.5% of its variation.
- VVIX is largely independent of the VIX term structure and the variance risk premium (VRP), which measures the difference between option-implied (expected) return variance and realized (actual) return variance.
- The slope component of the VVIX term structure relates positively to future returns of S&P 500 Index and VIX option straddles, and its predictive power is incremental to those of the slope of the VIX term structure and VRP.
- Gross median monthly returns for S&P 500 Index straddles are negative, ranging from -1.65% for 1-month maturity to -0.12% for 12-month maturity. Gross median monthly returns for VIX straddles are also negative, ranging from -1.87% for 1-month maturity to -0.26% for 5-month maturity.
- A trading strategy that is each day short (long) 1-month or 12-month S&P 500 Index straddles when the slope component of the VVIX term structure is in the bottom 75% (top 25%) of inception-to-yesterday values produces evenly spread signals and easily outperforms a short-only strategy, with gross annual Sharpe ratios:
- 1.50 for 1-month straddles, versus 1.20 for short-only.
- 1.09 for 12-month straddles, versus 0.30 for short-only.
- A similar strategy using the slope component of the VIX term structure produces clustered signals and gross annual Sharpe ratio 0.98 (0.51) for 1-month (12-month) S&P 500 Index straddles.
The following chart, taken from the paper, tracks the slope component of the VVIX term structure across 1-month, 3-month and 5-month maturities. The slope is quite volatile, with peaks coinciding with times of equity market turmoil.
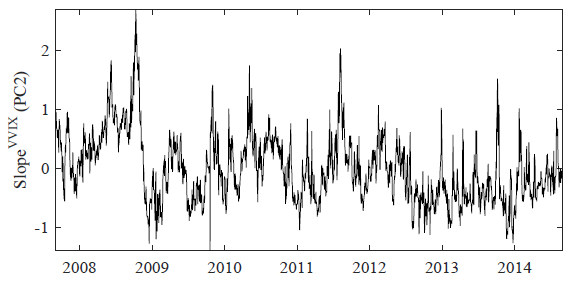
In summary, evidence indicates that the slope of the VVIX term structure may be a useful predictor of S&P 500 Index option straddle and volatility option straddle gross returns.
Cautions regarding findings include:
- Performance results are gross, not net. Accounting for the costs of monthly straddle portfolio reformation and daily long-short switching as signaled, which are likely material, would reduce reported Sharpe ratios.
- The tested S&P 500 Index straddle strategy is subject to snooping bias regarding choice of the VVIX term structure slope threshold for going long or short.
- Calculations required to support the tested straddle trading strategy are beyond the reach of most investors, who would bear fees for delegating them to an expert.
See also: