Reversion-to-Value (RTV) Model

Do investors require a predictably substantial expected stock market earnings yield (aggregate expected corporate operating earnings over the next 12 months divided by stock index level)? In other words, when the forward earnings yield is relatively high (low), do they bid stock prices up (down) to restore a normal expected yield. To investigate whether such a Reversion-to-Value (RTV) model works, we relate the evolution of an operating earnings forecast for the S&P 500 to the behavior of the S&P 500 Index. To convert from the quarterly earnings cycle to a monthly frequency, we assume 50% / 40% / 10% of new earnings data for a quarter becomes known during the first / second / third month after quarter end. Availability of S&P 500 lagged (trailing 12 month) operating earnings from Standard and Poor’s as an earnings forecast input limits the sample period. Using monthly earnings forecast and S&P 500 Index data during March 1989 through December 2011, we find that:

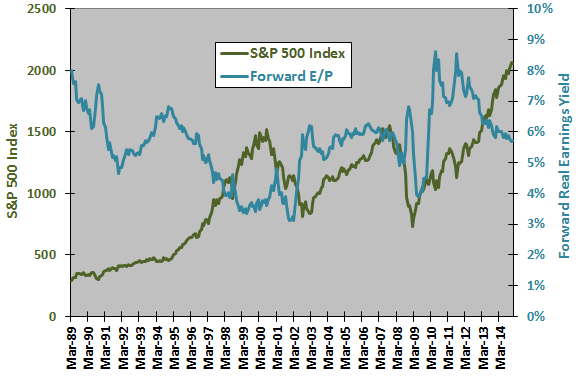
The following chart compares the S&P 500 Index and the S&P 500 forward earnings yield over the available sample period. The average forward earnings yield over this period is 5.54%, with monthly standard deviation 1.13%. Visual inspection suggests some tendency for the stock market to be relatively strong (weak) when the forward real earnings yield is high (low).

For precision, we relate the forward earnings yield to stock market returns over fixed future intervals.

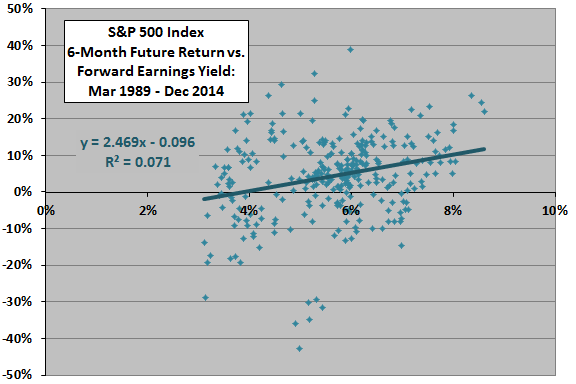
The following scatter plot relates the 6-month future return for the S&P 500 Index to the forward earnings yield over the available sample period. The Pearson correlation between the two series is 0.23 and the R-squared statistic is 0.06, indicating that the forward earnings yield explains 6% of the variation in 6-month future return. The positive slope indicates that future stock market returns tend to be higher (lower) when the forward earnings yield is relatively high (low).

Because the future return measurement interval (six months) is longer than the sampling frequency (monthly), the number of points on the scatter plot overstates effective sample size. Also, overlap of measurement intervals may distort statistics.

For a future return measurement interval of three (12) months, the Pearson correlation is 0.16 and the R-squared statistic is 0.03.

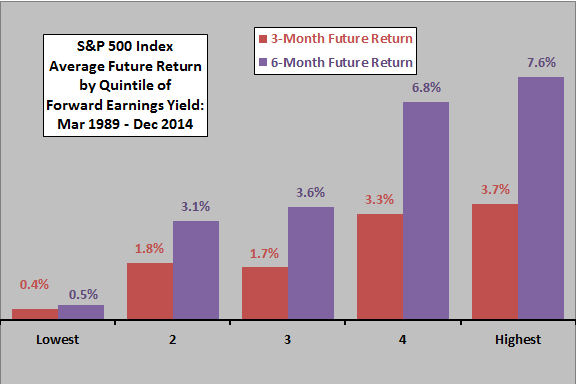
To investigate non-linearities, we calculate average future returns by ranges of the forward earnings yield.

The next chart summarizes the average 3-month and 6-month future returns for the S&P 500 Index by quintile of forward earnings yield over the available sample period. For both future return intervals, average returns increase somewhat consistently across forward earnings yield quintiles. Any lack of consistency is cautionary regarding model reliability.

There are about 54 observations per quintile, but overlap in return measurement intervals makes the sample very small for a quintile breakdown.

As a robustness test, we look at two subperiods.

Pearson correlations for the relationship between the 6-month future return for the S&P 500 Index and the forward earnings yield over two equal subperiods (March 1989 through April 2000 and May 2000 through June 2010) are 0.05 and 0.39. The disparity in correlations and the lack of correlation for the early subperiod undermine belief in model reliability. The overall sample period is short (compared to return intervals) for subperiod tests.

The (messy) linear relationship implied by the scatter plot above offers a way to estimate S&P 500 Index future returns. For example, based on data available through December 2011, the slope and y-intercept for the relationship between the S&P 500 Index 6-month future return and the forward earnings yield are 2.36 and -0.09, respectively. The forward earnings yield as of the end of December 2011 is about 7.94%. The projected return for the S&P 500 Index from the end of December 2011 through the end of June 2012 is therefore 2.36 * 7.94% – 9% = +9.5%.

A similar calculation for a 3-month horizon indicates a return of +4.5% from the end of December 2011 through the end of March 2012.

See Market Models for a summary of current stock market projections.

Note that the fairly wide dispersion of data points around the best-fit line in the above scatter plot indicates considerable variability in actual future returns. What might drive the dispersion? Possibilities include:

• Investors may employ methods of estimating forward earnings that differ materially from the Earnings Forecast used here.
• The U.S. stock market is not a closed system. Other, substantially uncorrelated earnings yields may compete.
• Decision factors other than real earnings yield (such as the inflation rate, as applied in the Real Earnings Yield Model) may be important to investors.
• There may be considerable randomness in market behavior.

In summary, the RTV Model appears to offer perhaps a little information about S&P 500 Index returns over the next few quarters, but it is not very reliable.

Some additional cautions regarding this conclusion are:

• As noted above, the effective sample size is fairly small for the tests employed, and overlap of measurement intervals may distort statistics.
• The available sample period may not be representative of the long-term relationship between S&P 500 Index future returns and the forward earnings yield.
• Non-normality of the stock market returns disrupts interpretation of “normal” statistics.

Research covered in Fundamental Valuation offers other perspectives on earnings valuation approaches.