Does pairs trading work for exchange-traded funds (ETF)? In their February 2010 paper entitled “Pairwise Asset Rotation Trading and Market Timing: An Anatomy to a New Trading Strategy”, Panagiotis Schizas and Dimitrios Thomakos present a market timing strategy based on transforming the predictability of relative returns/volatilities between pairs of ETFs into weekly trading signals via simple rules. They choose S&P Depository Receipts (SPY), the Financial Sector Select SPDR (XLF), PowerShares QQQ (QQQQ) and Oil Services HOLDRs (OIH) to investigate three pairs: SPY-XLF, SPY-QQQQ and SPY-OIH. For robustness, they consider weeks ending on Monday, Wednesday and Friday (for a total of nine pair-endpoint combinations). They consider five trading models based on relative pair returns, relative pair (realized) volatilities and more complex characterizations of relative pair performance. Relative return/volatility predictions derive from a rolling historical window of 104 weeks. Using daily open-high-low-close prices for SPY, XLF, QQQQ and OIH to construct weekly metrics from earliest availability through April 4, 2008, they conclude that:
- In many cases, the models considered yield statistically significant sign predictions for pair relative returns and relative volatilities.
- Based on terminal wealth and weekly Sharpe ratio, rotation models outperform both buying and holding one asset in a pair and an equal weighting of both assets in a pair for eight of nine pair-endpoint combinations. Models based on predictions of pair relative returns are best for six of nine combinations.
- A very simple pair trading model based on a moving average of relative returns can outperform both benchmarks.
- More elaborate pair trading models may perform even better than the five considered.
- Pair trading models are generally riskier than equal weighting of both assets in a pair, but a priori less risky than buying and holding one asset in a pair.
- Trading frequencies (and therefore trading frictions) vary considerably across the five pair trading models.
The following chart, taken from the paper, visualizes the estimated distributions of gross weekly returns for the five pairs trading models for the SPY-XLF pair and weeks ending on Fridays over the sample period. See the paper for precise definitions of the models.
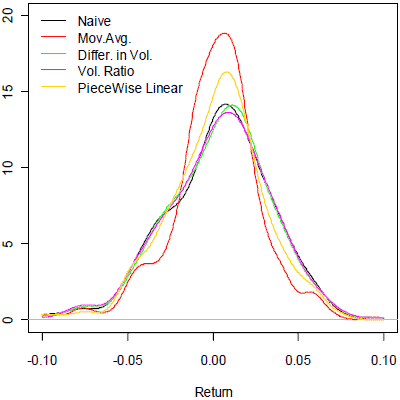
In summary, evidence from limited tests suggests that ETF pair trading based on relative returns/volatilities may outperform simple passive benchmarks.
Exclusion of trading frictions limits the persuasiveness of findings with respect to economic significance.
A reader asked: “I find it really hard to follow the academic language in the paper. Can you simplify?”
The strategy focuses on trading pairs from among four “broadly defined passive ETFs which we have selected based on criteria like market capitalization, long(er) historical tracking record, and high trading volume.” The anchor for each pair is S&P Depository Receipts (SPY). The second pair member is one of:
The authors use weekly closing prices to calculate weekly returns for each ETF. They use daily Open-High-Low-Close data to construct weekly volatility estimates for each ETF by summing relevant daily range-based estimates, with Formulas 1 and 2 in the paper specifying the exact method (some simpler volatility calculation may work). The authors then use a rolling 104-week window of past weekly return/volatility data for each of three pairs (SPY-QQQQ, SPY-XLF and SPY-OIH pair to forecast the difference in returns (relative return), volatilities and differences in volatility (relative volatility). The volatility and relative volatility forecasts in turn feed more complicated forecasts of relative return. The authors provide no rationale for the 104-week signaling interval.
The simplest pair trading scenario involves a weekly relative return forecast for an ETF pair based on the mean lagged difference in weekly ETF returns. For an ETF pair trading example that is comparable in simplicity to this naive scenario, see “Simple Gold-Gold Stock Fund Pair Trading”.
More complicated scenarios involve relationships between the relative return of an ETF pair for a given week and other lagged/forecasted variables. The discussion of Formula 9 in the paper summarizes predictive variables considered. These more complicated scenarios use regressions to estimate linear relationships between predictive variables and future pair relative returns. See “USING THE REY MODEL TO FORECAST U.S. STOCK MARKET RETURNS” and “USING THE RTV MODEL TO FORECAST U.S. STOCK MARKET RETURNS” for regression-based forecasts of comparable complexity.
For volatility forecasts, the authors quantify relationships between: current value of the weekly volatility for each ETF and its past weekly volatilities; and, the current relative volatility of an ETF pair and their past relative volatility. These autoregression-based forecasts are also comparable in complexity to the regression-based forecasts of the REY and RTV models. These volatility forecasts feed more complicated scenarios for forecasting the relative return for the ETF pair as described above.
For each relative return forecast scenario, the authors allocate funds to the ETF within a pair that has the higher forecasted return for the next week.
In summary, the method in the paper is to: (1) use rolling 104-week histories to forecast which of two ETFs will have the higher return next week; and, (2) allocate funds each week to the ETF with the higher forecasted return. The simplest forecast is essentially a narrow (two-asset) momentum strategy. The more complex forecasts derive from regressions of the relative return against a variety of potentially predictive variables.
The outcome of the strategy depends on both the behaviors of the two ETFs in the pair over the sample period and the strength of the relationship between the predictive variable used and the pair’s relative return.